DB1 - 관계 연산
| topics | 700-컴퓨터과학 |
| types | 레퍼런스 |
관계형 DB에서 릴레이션을 조작하기 위한 연산
- 실제 사용할 수 있는 데이터 언어는 아님
- SQL 언어나 내부처리의 이론적 기반을 제공
관계 대수
사용자가 필요로 하는 데이터를 획득하는 절차(HOW)
== 연산의 적용 순서를 명세
== 절차적 표현 방법
- 릴레이션을 내부적으로 처리하기 위한 연산의 집합.
- SQL의 이론적 토대를 제공
- 패쇄 성질
- 피연산자와 연산결과 모두 릴레이션
- 중첩된 수식표현이 가능
집합연산
릴레이션을 집합으로 간주하여 이를 처리하는 연산 그룹
예
- 합집합 UNION ∪
- 교집합 INTERSECT ∩
- 차집합 DIFFERENCE -
- 카티션 프러덕트 CARTESIAN PRODUCT x
- 릴레이션 R1과 R2의 각튜플을 서로 연결하여 만들어진 모든 튜플의 조합을 반환
- 두릴레이션의 모든 튜플을 수평적으로 결합하는 연산 (행렬의 곱과 비슷)
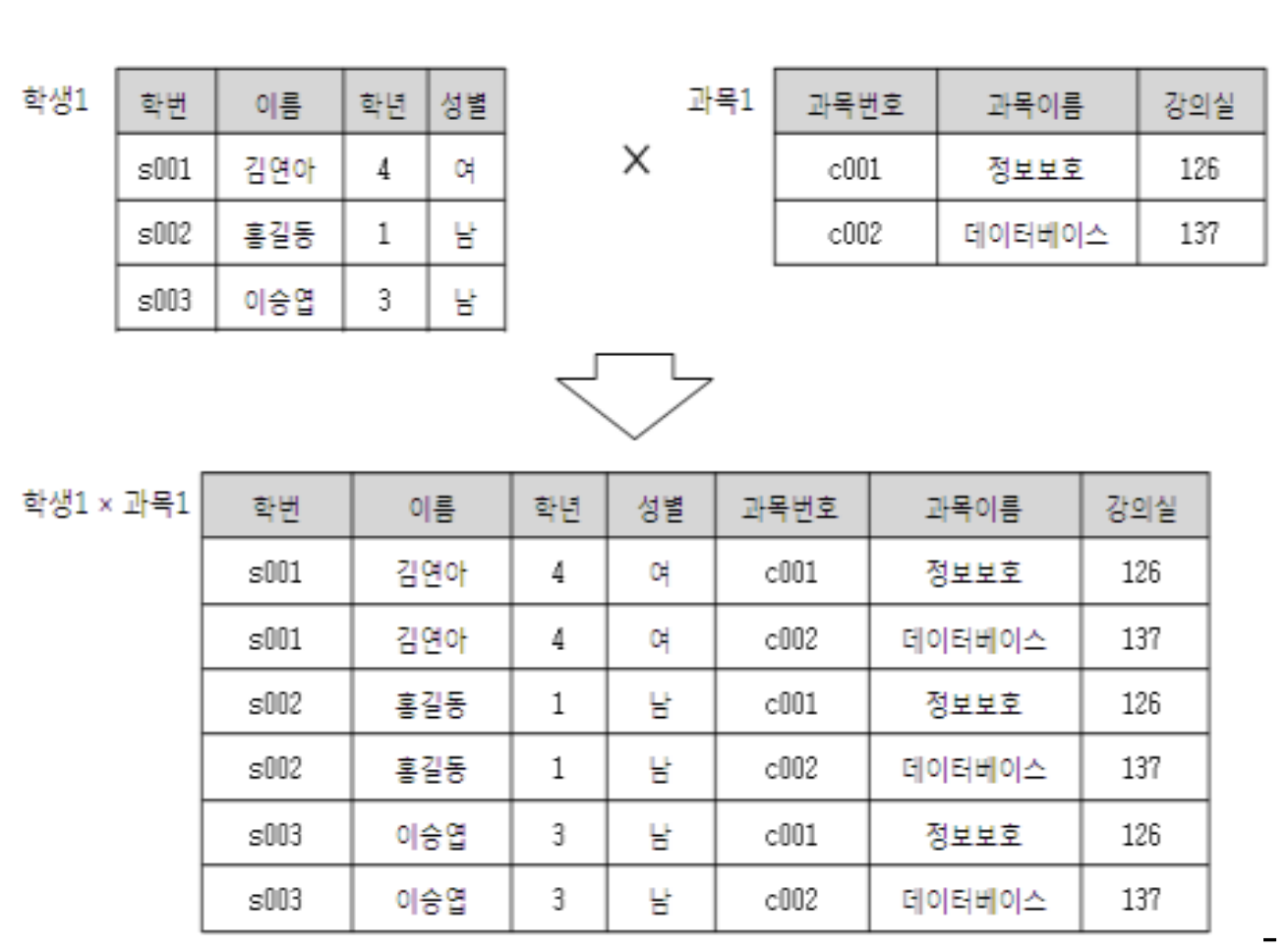
특징
- ∪, ∩, - : 합병가능
- 단 차수(속성의 개수)가 같아야함
- 대응 속성 쌍별로 도메인이 같아야함.
- ∪, ∩, × : 결합적, 교환적(집합에서 하던 결합법칙 교환법칙과 같음)
관계연산
릴레이션의 구조적 특성에 기반을 둔 연산을 포함
관계형 데이터 모델을 위해 고안된 연산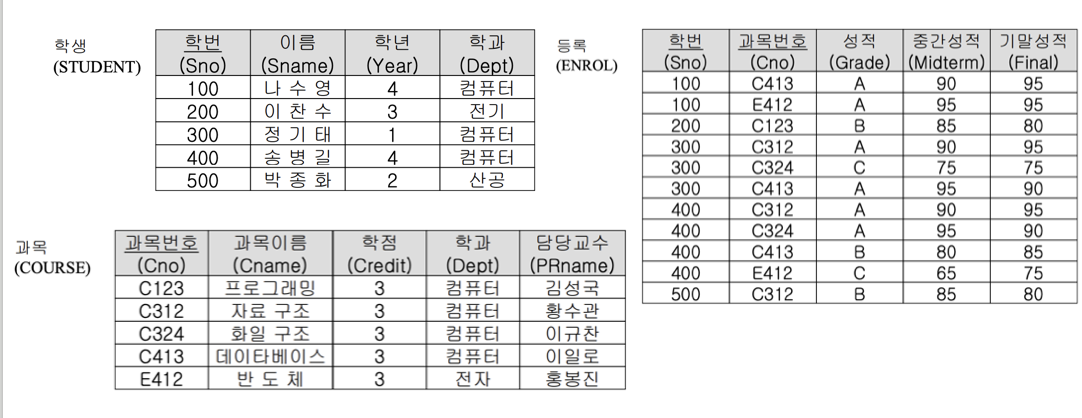
예
셀렉트 σ
- 선택 조건을 만족하는 릴레이션의 "수평적" 부분집합
- 데이터 언어 : R WHERE 조건식
- 선택도 : select 조건에 의해 검색되는 튜플의 비율
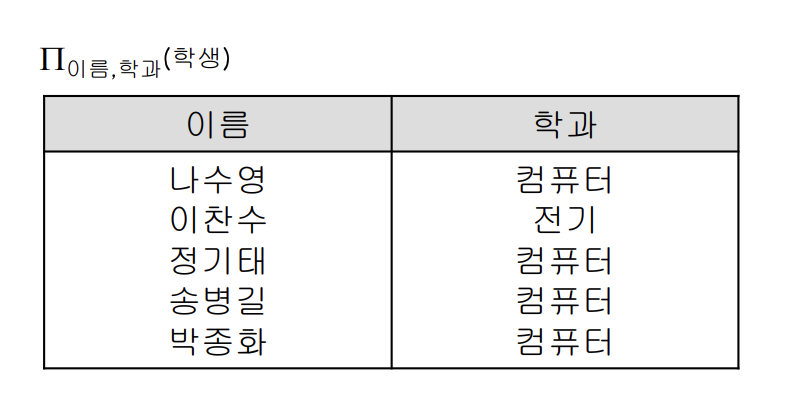
프로젝트 Π
- 릴레이션의 "수직적" 부분집합
- 결과에 튜풀이 중복시 제거
조인 ⋈
- 두 릴레이션의 공통속성 기준으로 조건을 만족시 수평적으로 결합
- 동등조인 아닌 세타조인은 조건있는 카디션 프러덕트 느낌 인것같다.
디비전 ÷
- 특정 값을 모두 찾고 있는 튜플을 찾는 연산
- R1÷R2 일시 R1이 R2의 모든 속성을 포함하고 있어야함
- R1 투플중 R2에 속한 속성을 제외한 나머지 속성값을 구성된 릴레이션.
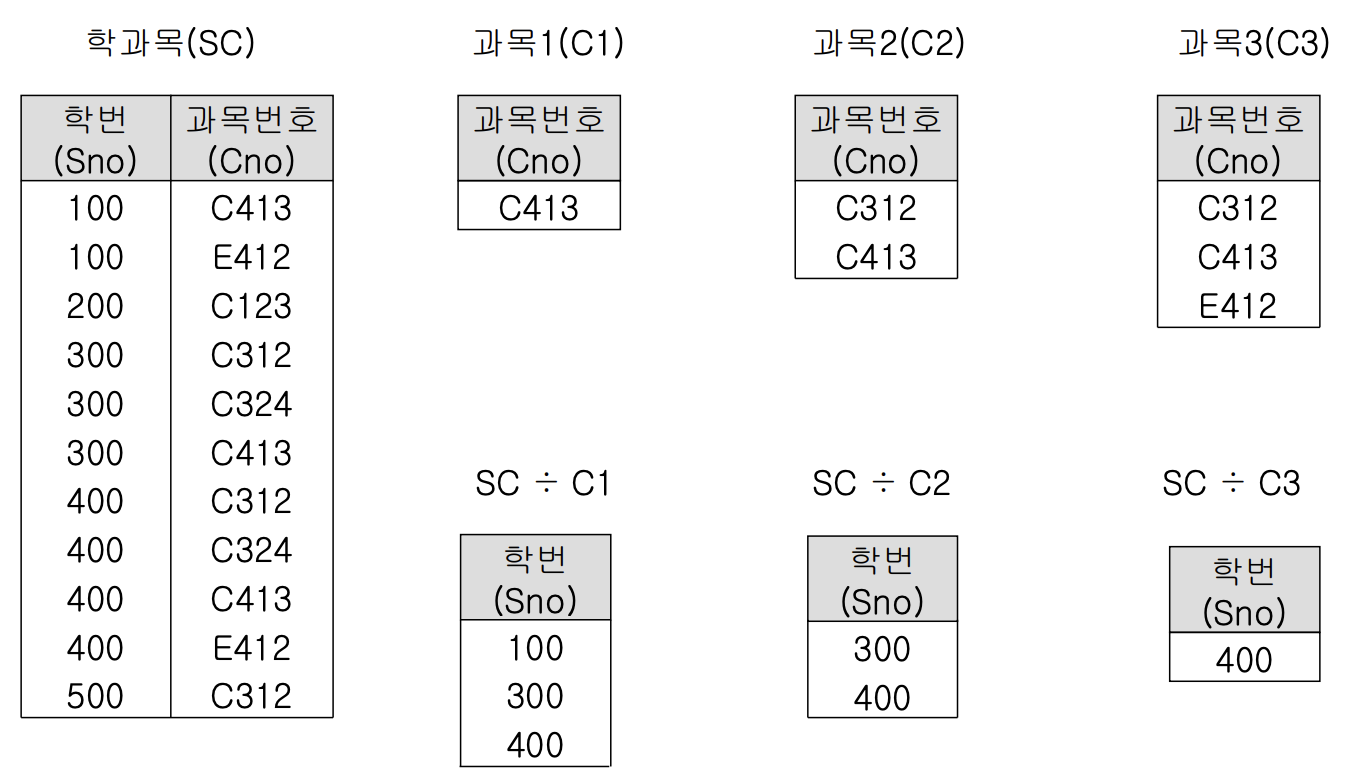
- R1 투플중 R2에 속한 속성을 제외한 나머지 속성값을 구성된 릴레이션.
개명연산 ρ
- 중간처리 결과 이름을 지정하거나 애트리뷰트 이름을 변경할 때 사용
대체 가능 여부
기본연산
다른 연산으로 대체 불가능
∪(합집합), −(차집합), ×(카티션 프로덕트), σ(셀렉트), Π(프로젝트)
복합연산
대체 가능
∩(교집합), ⋈(조인), ÷(디비전)
관계 대수의 확장
이후 예시를 위한 릴레이션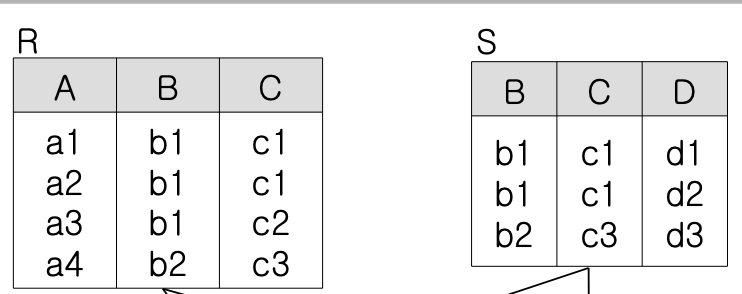
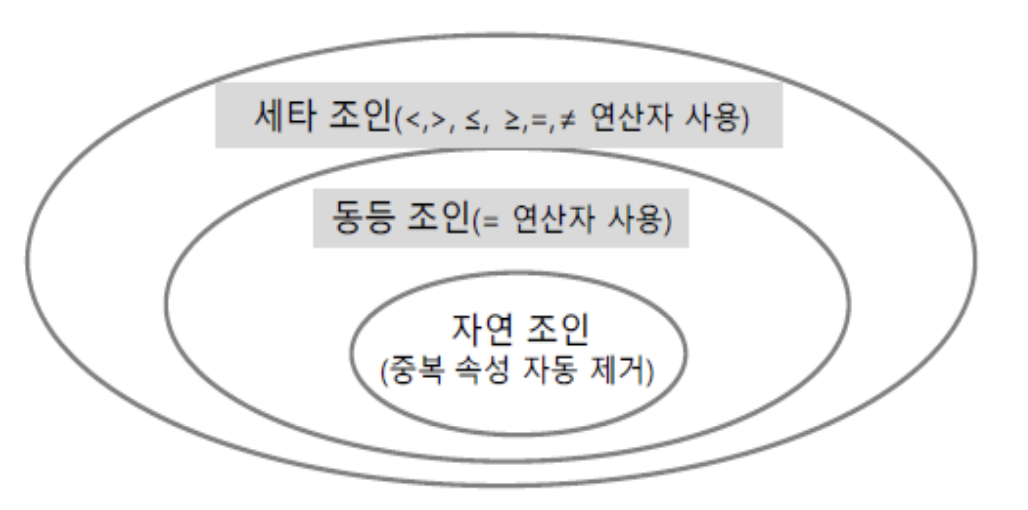
- 자연 조인 ⋈n
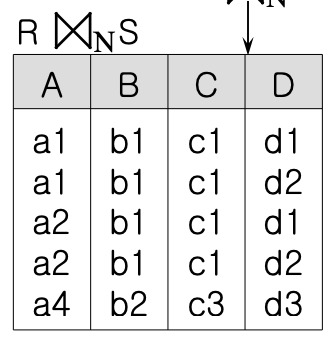
- 세미 조인 ⋉/⋊
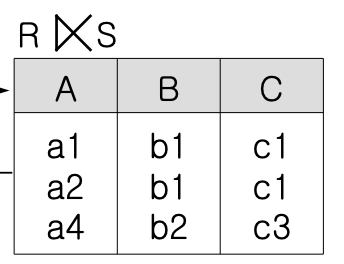 - R⋉S: S 와 자연조인이 가능한 R 투플의 집합.
- R에 흡수된느뀜
- R ⋉ S ≠ S ⋉ R
- R⋈nS = (R ⋉ S) ⋈n S = (S ⋉ R) ⋈n R
- R⋉S: S 와 자연조인이 가능한 R 투플의 집합.
- R에 흡수된느뀜
- R ⋉ S ≠ S ⋉ R
- R⋈nS = (R ⋉ S) ⋈n S = (S ⋉ R) ⋈n R - 외부 조인 ⋈+/⋉+/⋊+
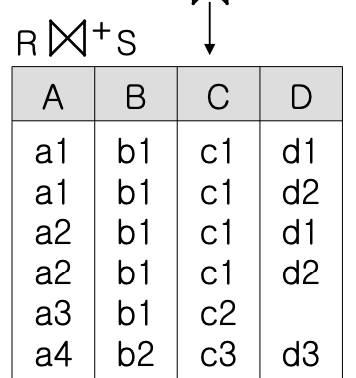 - 조인시 대응되는 튜플이 없을 경우에도 null값을 채워 결과 릴레이션에 포함
- 조인시 대응되는 튜플이 없을 경우에도 null값을 채워 결과 릴레이션에 포함 - 외부 합집합 ∪+
- AVG 평균
- GROUP 그룹화
관계 해석
사용자가 필요로 하는 연산의 최종 결과만 명세(WHAT)
== 선언적 표현방법
== 비절차적 표현방법
투플 관계 해석
요소
- 튜플 변수(= 범위 변수) : t
- 범위 릴레이션이 R일때, 범위식 R(t)
- 정량자 한정 여부
- 자유변수
- 속박변수
- 범위 릴레이션이 R일때, 범위식 R(t)
- 한정 애트리뷰트
- 투플 변수 t가 나타내는 투플의 애트리뷰트 A의
- 원자식 : t.A 또는 t[A]
- 구성요소
- 범위식 R(t)
- 조건식(한정애트리뷰트 + 비교연산자 +한 정애트리뷰트/상수)
- 실행결과는 항상 boolean
- 구성요소
- 정형식(WFF)
- 원자식, 불리언 연산자(∧,∨, ¬ ), 정량자 자 (∀,∃)가 다음규칙에 따라 결합된
- 불리언 연산자
- ∧ : AND
- ∨ : OR
- ¬ : NOT
- 정량자
- ∀ : 전체정량자
- ∀x : 모든 x에 대해서 ~한 조건을 만족하면 참, 아니면 거짓
- ∃ : 존재정량자
- ∃x : ~한 조건을 만족하는 것이 하나라도 있다면 참, 없으면 거짓
- ∀ : 전체정량자
- 규칙
- 원자식 ⊂ 정형식
- If F is WFF -> (F) 와 ¬F are WFF
- If F 와 G are WFF -> F∧G와 F∨G are WFF
- IF t is 자유변수 && F(t) is WFF -> ∀t(F(t))와 ∃t(F(t)) are WFF
- ㄹ