빅분기 3유형

topics	900-자격증 100-데이터분석 & AI
types	학습 이론
contexts	자격증
tags	#빅분기 #가설검정 #회귀분석 #카이제곱 #로지스틱회귀

빅분기 3유형 - 통계 분석

https://www.youtube.com/watch?v=aTAcJnch4gk&t=1169s
https://www.youtube.com/watch?v=dQkZwGfKUoY&t=743s

가설검정, 분산 분석, 카이제곱, 회귀, 로지스틱 회귀

np exp < -> np log
https://velog.io/@imymemineyay/%EB%B9%85%EB%8D%B0%EC%9D%B4%ED%84%B0-%EB%B6%84%EC%84%9D-%EA%B8%B0%EC%82%AC-%EC%8B%A4%EA%B8%B0-%ED%86%B5%EA%B3%84

https://doitforus.tistory.com/132#%EB%8C%80%EC%9D%91%20%ED%91%9C%EB%B3%B8%20%EA%B2%80%EC%A0%95-1

https://wikidocs.net/265436

import pandas as pd
import numpy as np
from scipy import stats
import statsmodels.api as sm

상관분석 : stats.pearsonr(simple['weight'],simple['height'])

검정접근로직

단일 표본 검정 (모집단 1개)
- 예) 과자의 무게는 200g과 다른지 검정
- ① 정규성 검정 : shapiro(data)
- ② 정규성 NO ) 비모수 검정 : wilcoxon(data - 기대값)
- ② 정규성 YES ) 단일 표본 검정 : ttest_1samp(data, 기대값)
대응 표본 검정 (모집단-같은 집단 2개)
- 예) 신약 효과 (전후) 검정
- ① 정규성 검정 : shapiro(data1 - data2)
- ② 정규성 NO ) 비모수 검정 : wilcoxon(data1, data2)
- ② 정규성 YES ) 단일 표본 검정 : ttest_rel(data1, data2)
독립 표본 검정 (모집단)
- 예) 1반과 2반의 성적 차이 검정
- ① 정규성 검정 : shapiro(data1), shapiro(data2) → 둘다 만족해야함
- ② 정규성 NO ) 비모수 검정 : mannwhitneyu(data1, data2)
- ② 정규성 YES ) 등분산 검정 : levene(data1, data2)
- ③ 등분산 NO ) 독립 표본 검정 : ttest_ind(data1, data2, equal_var = False)
- ③ 등분산 YES ) 독립표본 검정 : ttest_ind(data1, data2)

공식


# <span id="기본-양측검정-평균이-같냐다르냐"></span>기본 : 양측검정 : 평균이 같냐다르냐
# <span id="alternative-"></span>alternative 
# <span id="1-two-sided-대립가설의-내용이-서로-틀리다라고-주장할-때-사용-양측-검정"></span>1) two-sided: 대립가설의 내용이 서로 틀리다라고 주장할 때 사용. 양측 검정
# <span id="2-less-대립가설의-내용이-a-b-라고-주장할-때-사용-단측-검정"></span>2) less: 대립가설의 내용이, a < b 라고 주장할 때 사용. 단측 검정
# <span id="3-greater-대립가설의-내용이-a-b-라고-주장할-때-사용-단측-검정"></span>3) greater: 대립가설의 내용이 a > b 라고 주장할 때 사용. 단측 검정

# <span id="검정통계량-p-value"></span>검정통계량, p-value
## <span id="t-검정"></span>t-검정
# <span id="단일"></span>단일
t_stat, p_value = stats.ttest_1samp(df['weights'], 120)
# <span id="p_value-005-평균이-120이랑다름"></span>p_value < 0.05 :  평균이 120이랑다름
# <span id="독립"></span>독립
t_stat, p_value = stats.ttest_ind(data1, data2)
# <span id="p_value-005-평균이-둘이다름"></span>p_value < 0.05 :  평균이  둘이다름
# <span id="대응"></span>대응
st, pv = stats.ttest_rel(a, b)
# <span id="p_value-005-평균이-둘이다름"></span>p_value < 0.05 :  평균이  둘이다름


## <span id="f--검정"></span>f- 검정
f_stat, p_value = stats.f_oneway(group1, group2, group3)
# <span id="p_value-005-평균-분산차이-유의미"></span>p_value < 0.05 : 평균 분산차이 유의미

## <span id="비모수검정"></span>비모수검정
stats.wilcoxon(df['before'], df['after'], alternative = "less")

회귀분석(다중,로지스틱)

변수 선택, 회귀계수 해석, 예측값 산출, 성능평가(R², 오분류율 등)

COEF(회귀계수, regression coefficient)은 회귀분석에서 각 독립변수가 종속변수에 미치는 영향의 크기를 나타내는 값
- coefficients = result.params[1:] # 상수항 제외
  odds_ratios = np.exp(coefficients)
odds_ratio = np.exp(coef_high)
statsmodels.api 에서 param인자로 알수잇음
z-score : 어떤 데이터가 전체 평균에서 얼마나 떨어져 있는지를 "표준편차 단위"로 나타내는 값 절댓값이 클수록(0에서 멀수록) 좋다
P>|t| : p-value임
- 0.05 미만 : 변수가 종속변수에 통계적으로 유의미한 영향을줌
std err= 표준 오차 작을수록 굳
misclassification rate
- 1. (오분류 샘플 수) / (전체 샘플 수)

로지스틱 회귀

```python from statsmodels.formula.api import logit model = logit('disease ~ age + bmi', data=df).fit() print(model.summary())

import statsmodels.api as sm
X = sm.add_constant(df'age', 'bmi') # 상수항 직접 추가
y = df['disease'] model = sm.Logit(y, X).fit()
print(model.summary())

result = np. exp(coef1)
print(round(result, 1))

방법2) Statsmodels 라이브러리의 Logit 함수 적용

import statsmodels.api as sm
train_x_const = sm. add_constant(train_x)
model = sm. Logit(train_y, train_x_const) .fit(

상수항 추가

disp=0 옵션 사용 시 모델 학습 결과

coef1 = model params [ income ']
import numpy as np
result = np. exp(coef1)
print(round (result, 1))

방법3) statsmodels 라이브러리의 GLM 함수 적용

import statsmodels.api as sm

train_x_const = sm.add_constant(train_x)

상수항 추가

model = sm.GLM(train_y, train_x_const, family=sm.families.Binomial)).fit()

Log-Likelihood = llf
    로그우도(모델 적합도), 절대값이 작을수록 적합도가 높음
Df Residuals: 997  
    잔차 자유도(1000 - 3, Intercept 포함)
    높을수록조음용
LLR p-value: 1.984e-15  
    전체 모델의 유의성 검정, p<0.05이므로 모델이 통계적으로 유의함
Pseudo R-squ.: 0.04996  
    의사결정계수(로지스틱 회귀의 설명력, 0.05로 낮은 편)
- **  회귀분석(다중, 로지스틱)**: 까지 연습 필요.

### <span id="glm"></span>glm

import statsmodels.api as sm
glm_binom = sm.GLM(y, X, family=sm.families.Binomial())
result = glm_binom.fit()
print(result.summary())

- **잔차 이탈도, deviance 등 GLM에서만 제공되는 지표를 물을 때**
    - 예: "잔차 이탈도를 구하시오", "모델의 deviance 값을 해석하시오" 
- **시험 문제에서 "일반화 선형모형" 또는 "GLM"이라는 단어가 직접적으로 언급될 때**
정확하진 않지만 제가 강의 들었을 때는 logit은 summary에 잔차이탈도가 안나오는데 glm은 나와서 잔차이탈도 구할때만 glm을 썼어요!
- 즉, Deviance:: ㅌ**잔차이탈도 = 각 관측치의 실제값과 예측값이 얼마나 다른지, 이탈도 관점에서 측정한 값**입니다.
## <span id="카이제곱-검정"></span>카이제곱 검정
chi
- **카이제곱 검정**: 교차표, 기대빈도, 카이제곱 통계량, p-value 해석 등 실전 계산 연습 필요.
### <span id="독립성"></span>독립성
두변수가 독립인지
```python
import numpy as np
from scipy.stats import chi2_contingency

# <span id="교차표관측-빈도"></span>교차표(관측 빈도)
# <span id="흡연-비흡연"></span>흡연  비흡연
# <span id="남자-30-20"></span>남자   30     20
# <span id="여자-10-40"></span>여자   10     40
data = np.array([[30, 20],
                 [10, 40]])

# <span id="카이제곱-검정-실행"></span>카이제곱 검정 실행
chi2_stat, p_value, dof, expected = chi2_contingency(data)

print(f"카이제곱 통계량: {chi2_stat:.4f}")
print(f"p-value: {p_value:.4f}")
print(f"자유도: {dof}")
print("기대빈도표:")
print(expected)

# <span id="해석"></span>해석
alpha = 0.05
if p_value < alpha:
    print("귀무가설 기각: 두 변수는 독립이 아님(연관 있음)")
else:
    print("귀무가설 채택: 두 변수는 독립임(연관 없음)")

적합도

이론적 분포와의 비교

from scipy.stats import chisquare

# <span id="관측-빈도-예-6면-주사위-60번-던짐"></span>관측 빈도 (예: 6면 주사위 60번 던짐)
observed = [8, 9, 10, 11, 12, 10]
# <span id="기대-빈도-공정하다면-각-면이-10번씩-나와야-함"></span>기대 빈도 (공정하다면 각 면이 10번씩 나와야 함)
expected = [10, 10, 10, 10, 10, 10]

chi2_stat, p_value = chisquare(f_obs=observed, f_exp=expected)

print(f"카이제곱 통계량: {chi2_stat:.4f}")
print(f"p-value: {p_value:.4f}")

if p_value < 0.05:
    print("귀무가설 기각: 주사위는 공정하지 않음")
else:
    print("귀무가설 채택: 주사위는 공정함")


import pandas as pd
from scipy import stats
import statsmodels.api as sm
import numpy as np
# <span id="indexresistin-classification-dtypeobject"></span>Index(['Resistin', 'Classification'], dtype='object')
df = pd.read_csv("data/bcc.csv")

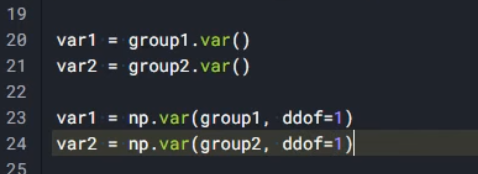
group1 = df[df['Classification']==1]['Resistin']
group2 = df[df['Classification']==2]['Resistin']

g1 = np.log(group1)
g2 = np.log(group2)

n1 = len(g1) - 1
n2 = len(g2) - 1

print(stats.f_oneway(g1,g2))
print(stats.ttest_ind(g1,g2))

sum_var = (np.var(g1)*n1 + np.var(g2)*n2)/(n1+n2)
print(sum_var)
# <span id="printdirstats"></span>print(dir(stats))

# <span id="해당-화면에서는-제출하지-않으며-문제-풀이-후-답안제출에서-결괏값-제출"></span>해당 화면에서는 제출하지 않으며, 문제 풀이 후 답안제출에서 결괏값 제출

> F_onewayResult(statistic=9.172465158846453, pvalue=0.003039226943143336)
TtestResult(statistic=-3.0286077921788537, pvalue=0.0030392269431433142, df=114.0)
0.4413710541719135

예시

회귀부분

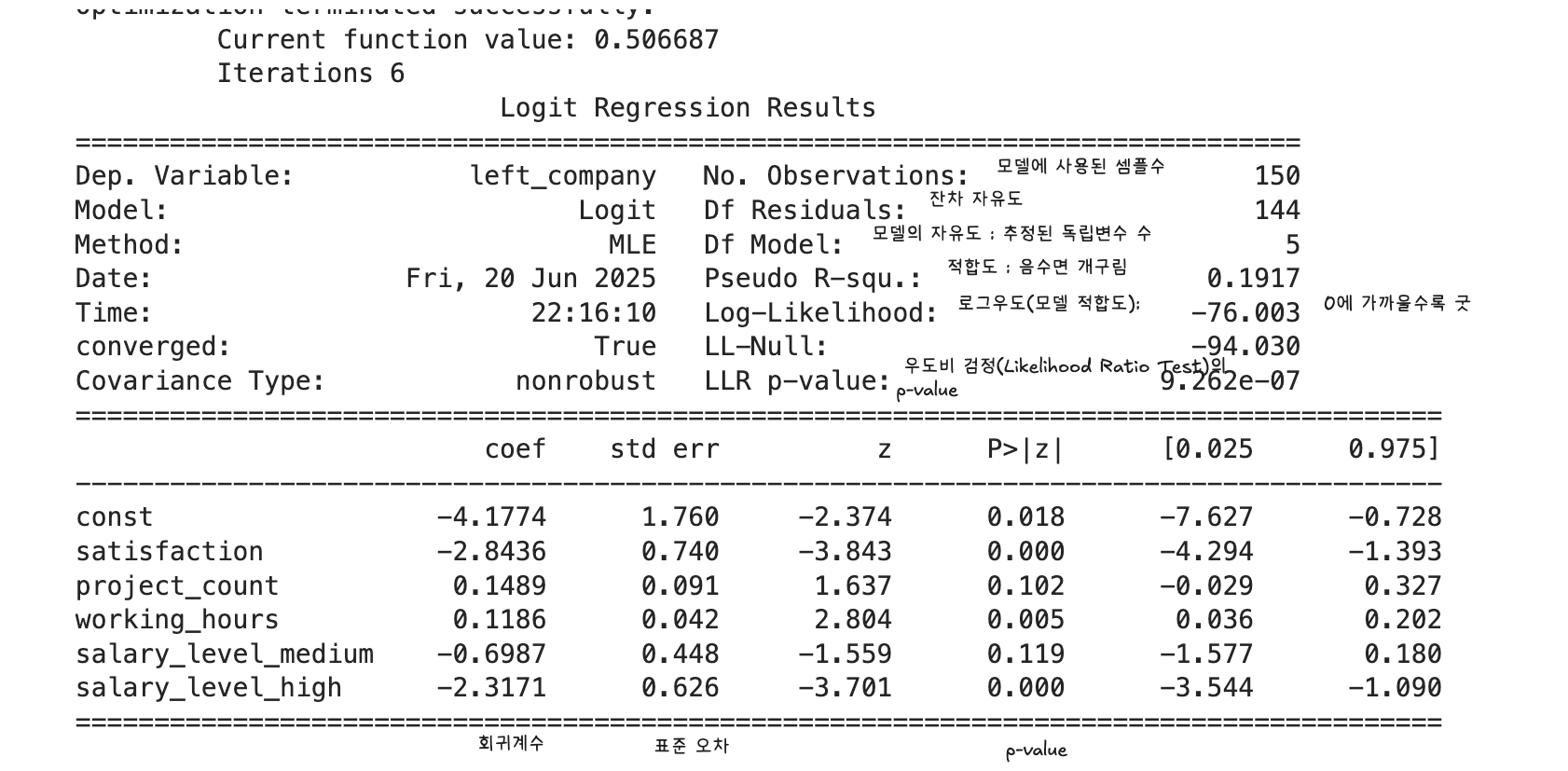
# <span id="데이터-불러오기"></span>데이터 불러오기
# <span id="독립변수-satisfaction-salary_level-project_count-working_hours"></span>독립변수: satisfaction, salary_level, project_count, working_hours

# <span id="종속변수-left_company-퇴사-여부-0-재직-1-퇴사"></span>종속변수: left_company (퇴사 여부: 0 = 재직, 1 = 퇴사)

# <span id="salary_level은-범주형-변수이며-기준-수준reference-level은-low로-설정합니다"></span>salary_level은 범주형 변수이며, 기준 수준(reference level)은 low로 설정합니다.
import pandas as pd
import numpy as np
import pandas as pd
import statsmodels.api as sm
df = pd.read_csv('/kaggle/input/bigdatacertificationkr/employee_attrition.csv')
df.head()
y= df['left_company']
x= df.drop(columns = ['left_company'])
x['salary_level'] = pd.Categorical(
    x['salary_level'], 
    categories=['low', 'medium', 'high'], # **첫 번째 요소('low')를 참조 수준**으로 자동 설정
    ordered=False
)
x = pd.get_dummies(x,drop_first=True, dtype=int)

# <span id="printhelpsmlogit"></span>print(help(sm.Logit))
x_const = sm.add_constant(x)
print(x_const.head())
model = sm.Logit(y,x_const).fit()
model.summary()


# <span id="문제-2-1-satisfaction-회귀계수"></span>문제 2-1: satisfaction 회귀계수
coef_satisfaction = model.params['satisfaction']
rounded_coef = round(coef_satisfaction, 3)
print(f"문제 2-1: satisfaction 회귀계수 = {rounded_coef}")

# <span id="문제-2-2-salary_levelhigh-오즈비"></span>문제 2-2: salary_level=high 오즈비
coef_high = model.params['salary_level_high']
odds_ratio = np.exp(coef_high)
rounded_odds = round(odds_ratio, 3)
print(f"문제 2-2: high vs low 오즈비 = {rounded_odds}")

# <span id="문제-2-3-정밀도-계산"></span>문제 2-3: 정밀도 계산
y_pred_prob = model.predict(x_const)
y_pred = (y_pred_prob >= 0.5).astype(int)
precision = precision_score(y, y_pred)
rounded_precision = round(precision, 3)
print(f"문제 2-3: 정밀도 = {rounded_precision}")
# <span id="satisfaction"></span>satisfaction
# <span id="1--28436-"></span>1. -2.8436

문제 2-1: satisfaction 회귀계수 = -2.844
문제 2-2: high vs low 오즈비 = 0.099
문제 2-3: 정밀도 = 0.622

카이제곱

from scipy.stats import chi2_contingency 

## <span id="교차표가-필요함"></span>교차표가 필요함
table = pd.crosstab(df['Gender'],df['Survived'])
chi2_contingency(table)
stat , p ,df ,expect = chi_contingency(table)
print(round(stat,3))

# <span id="2번"></span>2번

from statsmodels.api import Logit
from sklearn.preprocessing import LabelEncoder
import statsmodels.api as sm

encoder = LabelEncoder
df[ 'Gender'] = encoder.fit_transform(df[ 'Gender' ])

X = df<a href="/pages/'Gender'%2C-'SibSp'%2C-'Parch'%2C-'Fare'.html" class="wiki-link">'Gender', 'SibSp', 'Parch', 'Fare'</a>

X = sm.add_constant (X)

y = df[ 'Survived' ]

model = Logit (y, X)

results = model. fit()

print(results.summary))
import numpy as np

print(round(p. exp(-0.3539))