DB1 - 종속성과 정규화
| topics | 700-컴퓨터과학 |
| types | 레퍼런스 |
데이터베이스 스키마는 데이터베이스의 테이블, 열 및 해당 유형을 정의함
릴레이션 스키마 설계
- 애트리뷰트 엔티티 관계성을 파악, 제약조건(종속성을 수집)
- 관련 애트리뷰트를 릴레이션으로 분할하고 묶음 = 스키마 변환
- 애트리뷰트간의관계성: 데이터 종속성
- 효율적인 데이터 처리
- 데이터의 일관성
- 변칙적 성질 예방 - 이상
스키마 변환
- 정보 표현의 무손실
- 최소의 데이터 중복
- 분리의 원칙 : 독립된 관계성은 별도로 분리시켜 표현
이상
원인
하나의 개체에 속한 속성간에 존재하는 여러개의 종속관계를 하나의 릴래이션으로 표현하기 때문
해결
속성들 간의 여러 종속관계를 분해하여 각각 하나의 릴레이션으로 표현
=> 정규화 : 잘못된 스키마 정의를 바로 잡는 db설계 방법
종류
EX) 한 릴레이션에 학번, 과목번호, 성적, 학년이 있을 때! 기본키: 학번,과목
삭제 이상
연쇄 삭제에 의한 정보 손실
한 학번이 과목 등록을 취소햇을 시 -> 학년의 정보도 삭제됨!
삽입 이상
원하지 않은 정보 강제 삽입
한 학생이 2학년이라는 사실 만 삽입하고 싶을 때 불가능
갱신이상
중복데이타의 일부 갱신으로 정보의 모순성이 발생
한 학생의 학년을 4에서 3으로 변경 -> 해당학생의 투플을 모두 변경해야함.
함수종속(FD)
정의
릴레이션 R과 R의 속성중에 하나인 X,Y 가있음
X의 각각 값에 대해 Y 값이 하나만 있을 때가 함수종속이라함.
X에 의해 Y값이 정해진다.
X->Y로 표현, X: 결정자 Y: 종속자
X,Y는 속성의 집합이 될 수 있음
고로 PK는 그외의 속성 집합에 대해 함수종속ㅋ
근데 X가 키는 아님: X 값 20 이고 Y 값 40 인 튜플이 두개 수 있다는 것임
함수종속 다이어그램
수강(학번, 과목번호, 학년, 성적) : PK{학번,과목번호}
{학번,과목번호} -> 성적
학번 - > 학년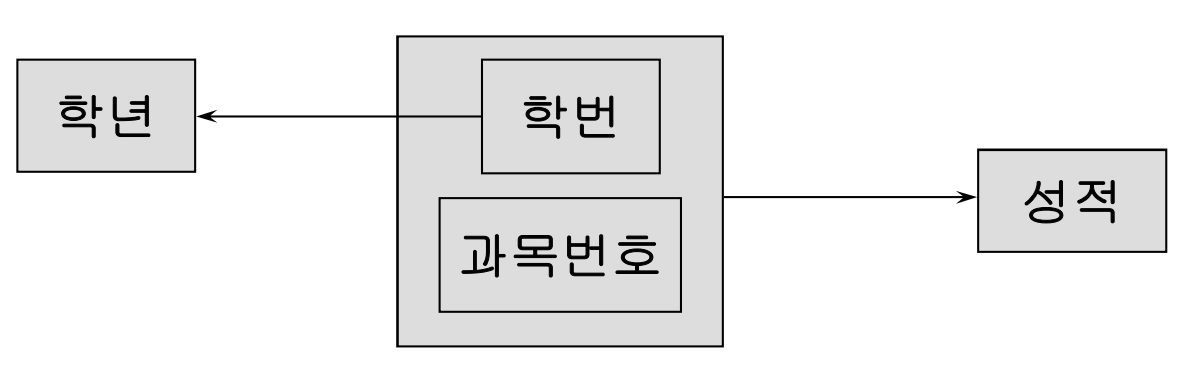
종류
완전 함수 종속
결정자집합에서 머하나 빼면 함수종속이 아니게되는것
X’ ⊂ X 이고 X’ -> Y 가 성립되는 애트리뷰트 X'이 존재하지 않는 경우
부분 함수 종속
결정자 집합 중속성하나 자체도 함수종속이 되는것.
X’ ⊂ X 이고 X’ -> Y 가 성립되는 애트리뷰트 X'이 존재하는 경우
위의 예시로보면 학년은 {학번,과목번호}에 부분종속
정규형
일련의 제약조건을 만족하는 릴레이션
정규화 과정에서 릴레이션이 만족해야하는 특정한 함수 종속성의 충족 요건
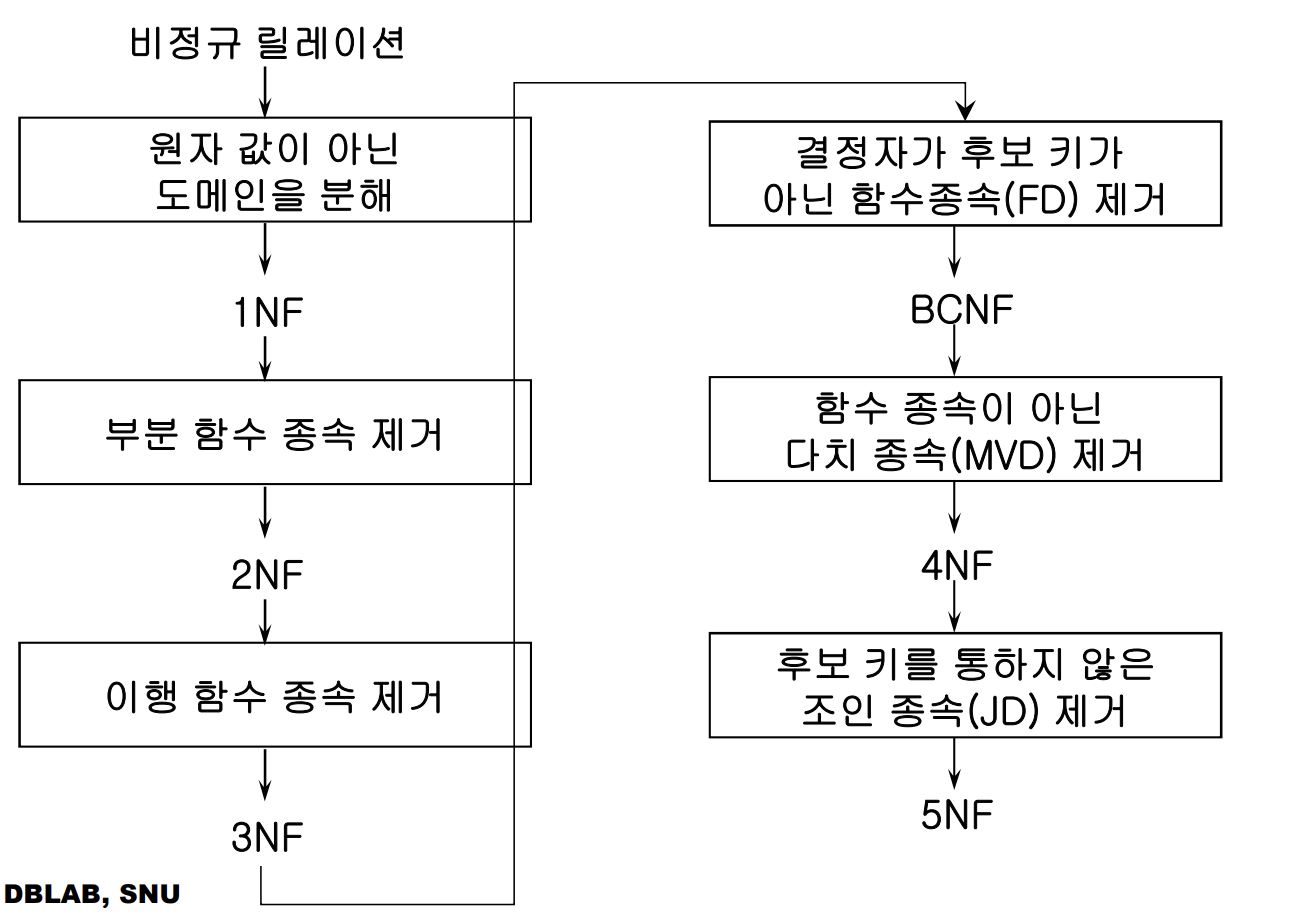
정규화 : 스키마 변환으로 정규형을 만듬
정규화 원칙
- 정보 표현의 무손실
- 같은 의미의 정보 유지
- 효율적인 구조
- 최소 데이터 중복
- 분리의 원칙
- 독립적인 관계는 별개의 릴레이션으로 표현
종류
3NF이상이면 충분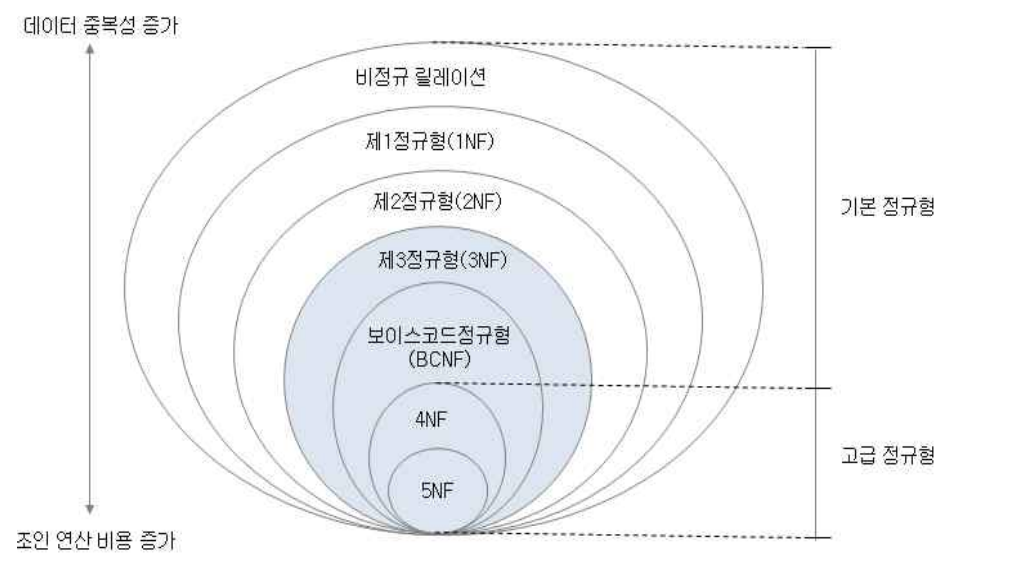
정규형에 쓸 예시(1NF의 상태임)
수강지도(학번,지도교수,학과,과목번호,성적)
기본키 : {학번, 과목번호}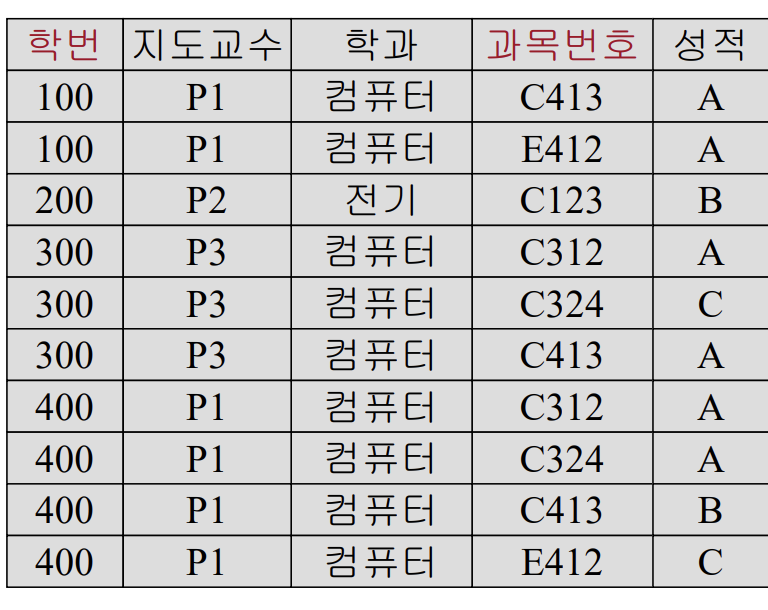
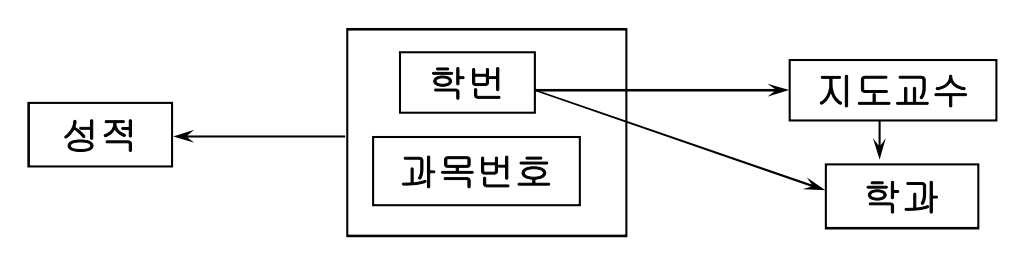
제 1정규형 (1NF)
모든 도메인(속성)이 원자값으로만 된 릴레이션
이상
- 삽입이상 : 500번 학번의 지도교수를 삽입할때 과목과성적을 넣어야만함
- 삭제이상 : 200번학생이 C123등록 취소하여 튜플 삭제시 지도교수 정보까지삭제
- 갱신이상 : 400번학생의 지도교수를 변경시 튜플 4개를 다바꿔야함
- 원인 기본키로 식별되는 개체와 무관한 애트리뷰트가 존재 = 독립적인 속성이 하나의 릴레이션으로 표현
제 2정규형 (2NF)
1NF에서 부분함수 종속을 제거 : 프로덱션으로
다이어그램으로 생각하면 사각형에 화살표 뻗어나가는 박스끼리 분리
지도(학번,지도교수,학과) PK:학번
수강(학번, 과목번호, 성적) PK{학번(FK), 과목번호}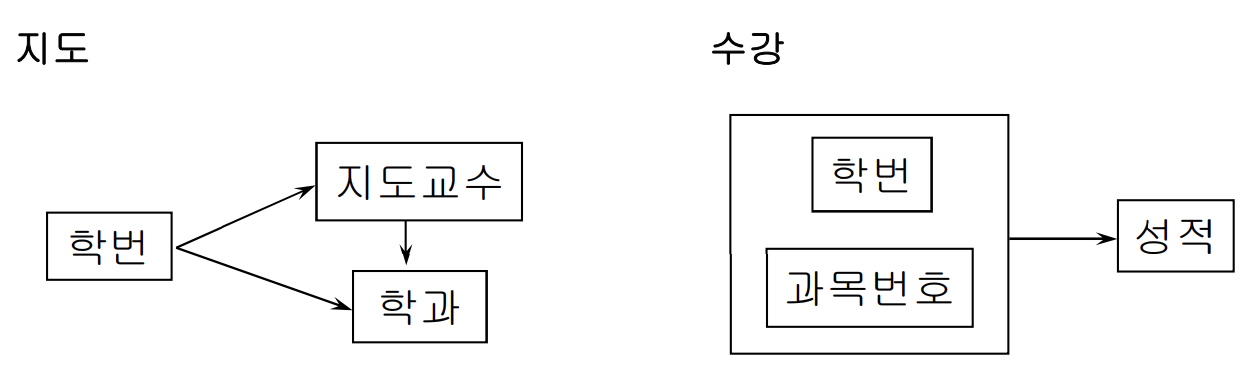
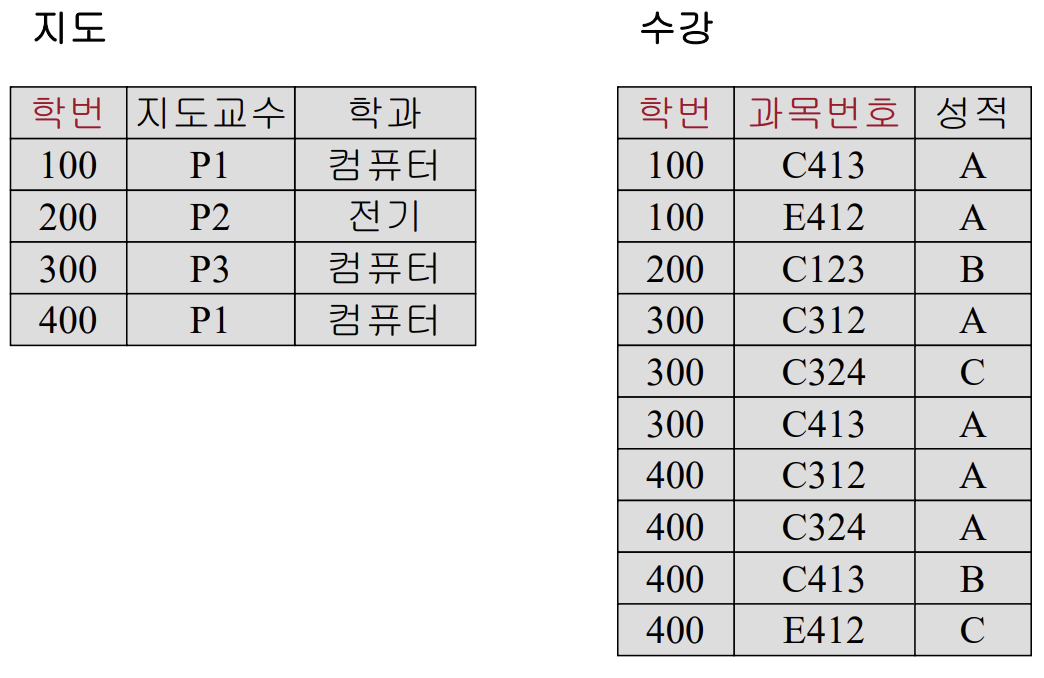
무손실 분해
 . 조인을통해서 1NF모형을 고대로 얻을 수 있음.
1NF에서 2NF의 정보를 모두 얻을 수 없음(2NF가 더 많을 수 있음)
. 조인을통해서 1NF모형을 고대로 얻을 수 있음.
1NF에서 2NF의 정보를 모두 얻을 수 없음(2NF가 더 많을 수 있음)
이상
- 삽입이상 : 어떤 지도가 특정 학과에 속하는사실이 삽입 불가능
- 삭제이상 : 300번 학생의 튜플 삭제시 지도교수가 어떤학과에 속한다는 정보상실
- 갱신이상 : 지도교수 소속을 변경시 학번튜플 여러개를 변경해야함
- 원인 : 이행적 함수 종속이 존재
- X → Y (X가 Y를 결정한다, Y → Z (Y가 Z를 결정한다)
- 꼬리에 꼬리를 무는 함수 종속
제 3정규형(3NF)
이행적 함수 종속 분리 : 꼬리에 꼬리를 무는 화살표제거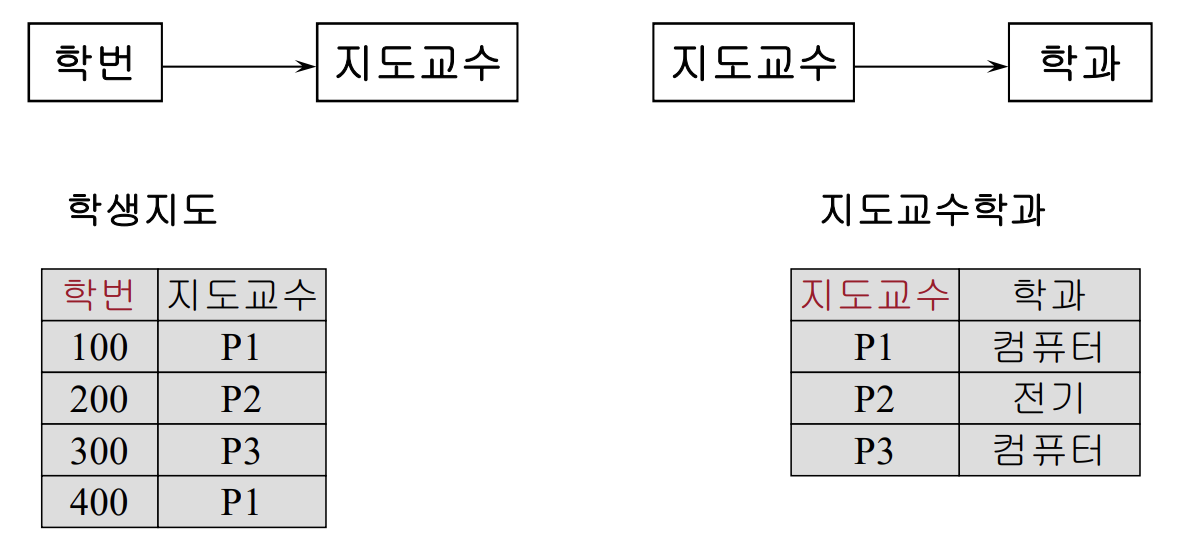
무손실 분해

이상
키가 아닌 애트리뷰트 값 갱신시 불필요한 이상은 발생하지 않음
적용이 불가능한 경우
- 복수의 후보키 가지고 잇음
- 후보는 두개이상의 속성으로 구성
- 후보키의 속성이 서로 중첩
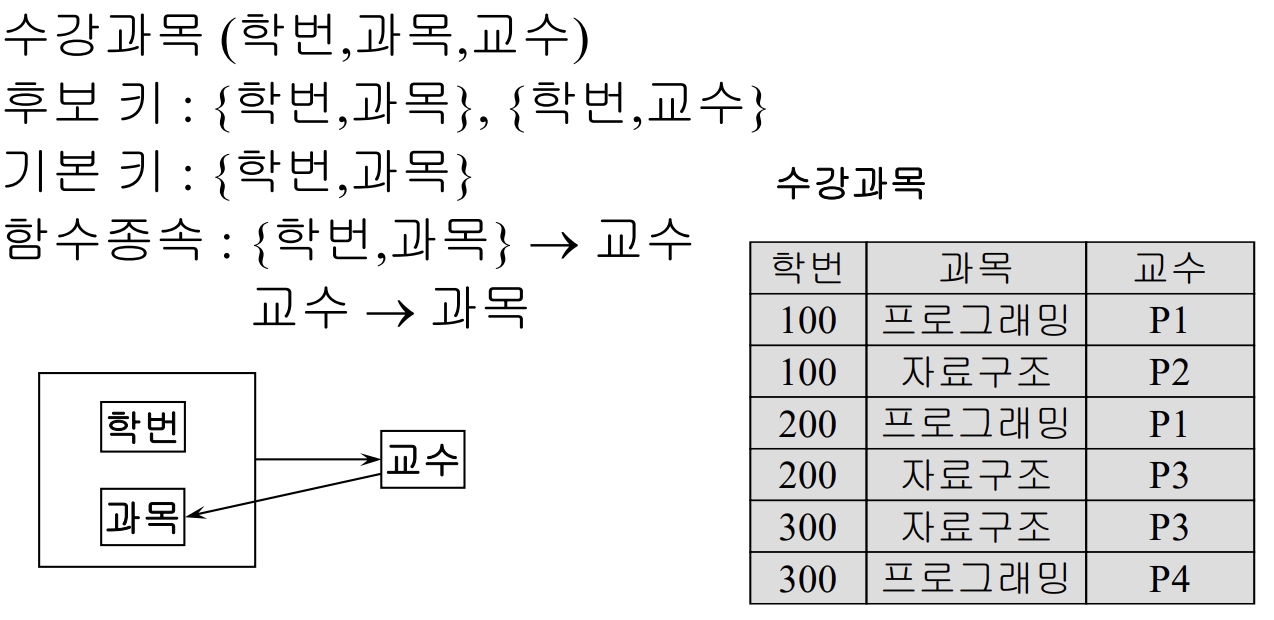
- 이때의 상태이상
- 삽입이상 : 교수 어떤 과목을 담당하는 정보를 넣을때 학번이 있어야함
- 삭제이상 : 학생이 과목취소하면 교수정보까지 날아감
- 갱신이상 : 교수가 과목을 바꾸면 해당 정보를 담고잇는 모든 튜플을 바꿔야함
- 원인 : 교수가 결정자지만 후보키가 아님
보이스/코드 정규형(BCNF)
= 강한 3NF
⊃ 1NF, 2NF ,3NF
한 릴레이션의 결정자가 모두 후보키면 BCNF에 속함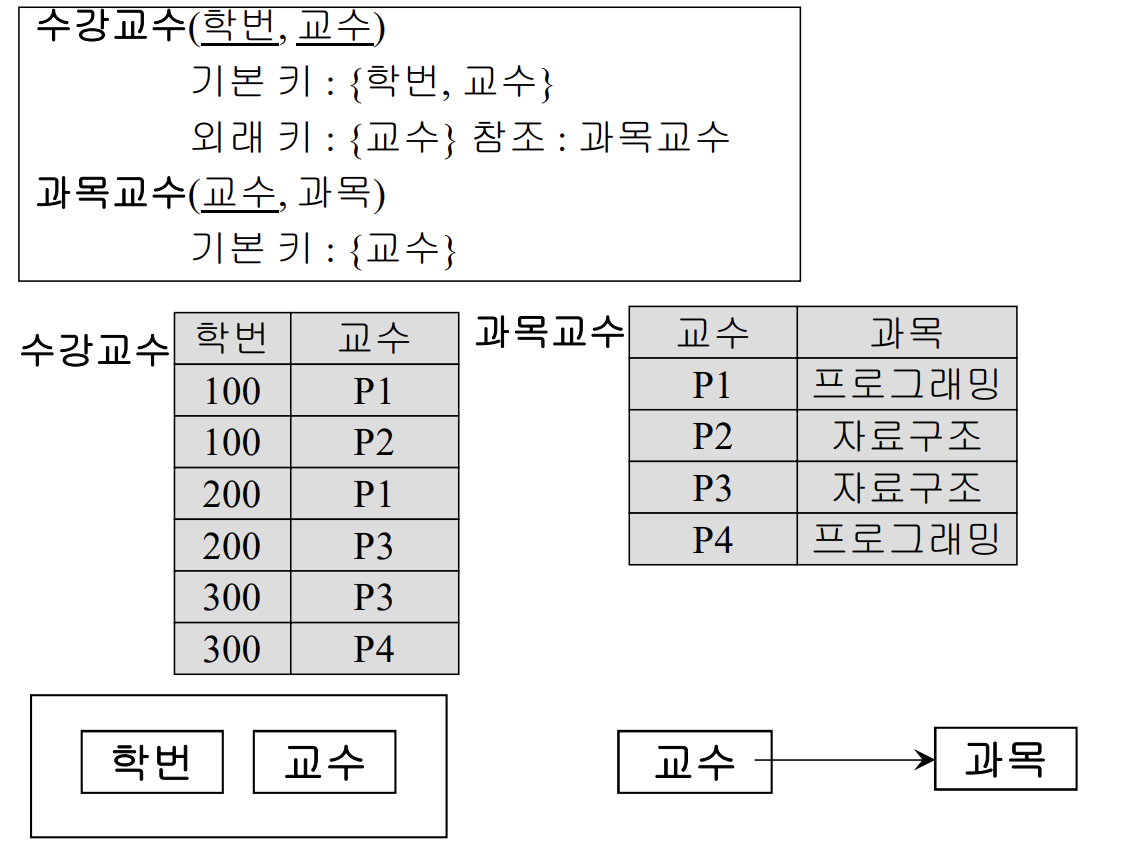
- 3NF여도 기본키 속성이 기본키 속성이 아닌 일반속성에 종속적일 때 BCNF정규형에 위반
- 문제풀어보기

제 4정규형(4NF)
BCNF에 속하고 모든 MVD가 FD다.(MVD가 없어도 됨.)
- 어떤 릴레이션 R이 4NF이라면 MVD가 없거나, MVD A B|C가 있을 경우 A에 대응되는 B와 C의 값은 하나씩 이어야 하며 이때 A는 후보키라는것을 의미한다.
MVD : 다치종속
특정 속성 A가 속성 B의 값의 집합을 결정한다.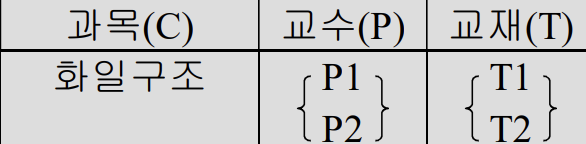
모든 FD는 MVD이다.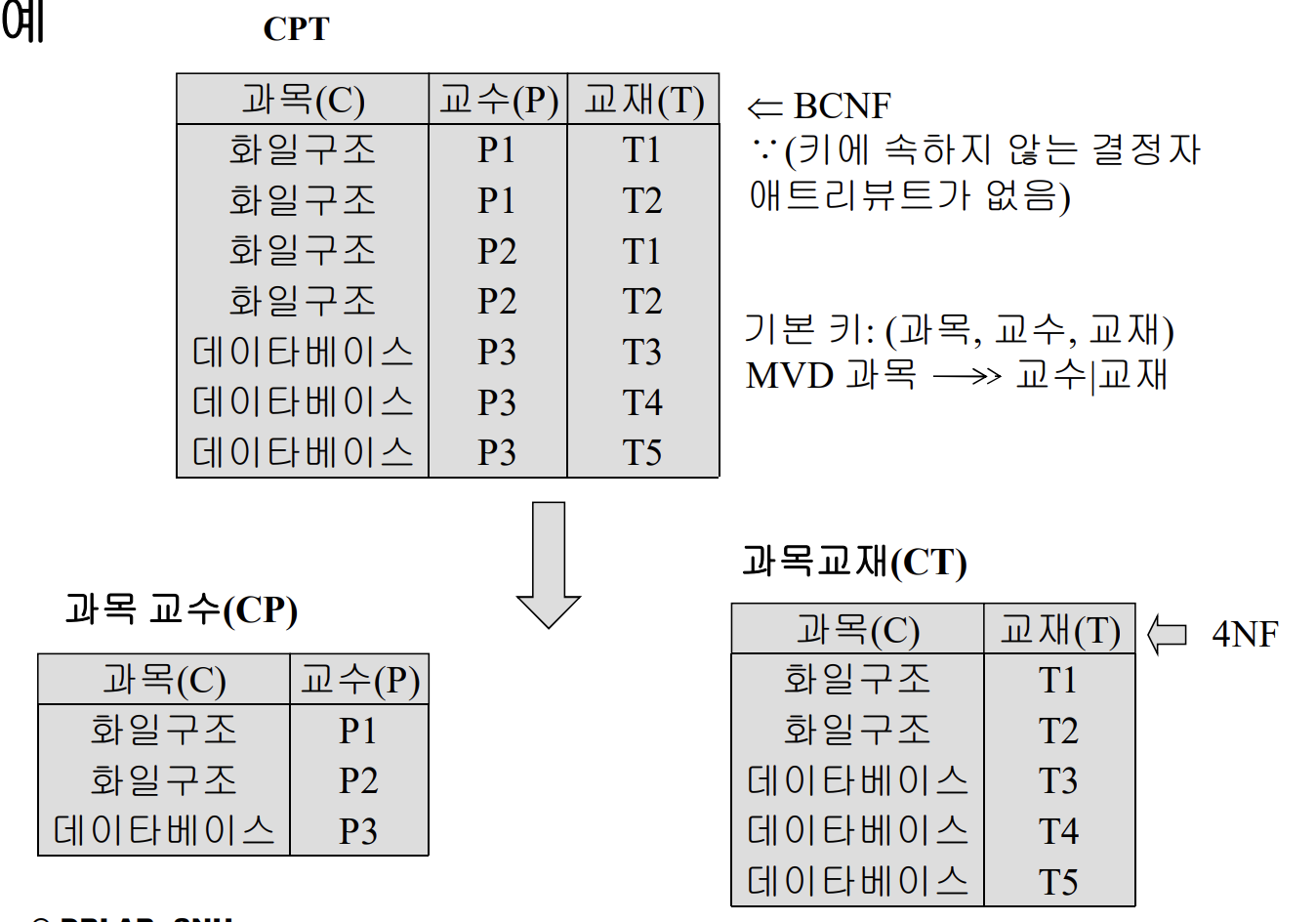
제 5정규형(5NF,PJ/NF)
R에 존재하는 모든 조인 종속이 R의 후보키를통해 성립됨
SC, CP ,PS : 어떠한 조인 종속 포함 ㄴㄴ == 5NF
SCP(SN,CN,PN) 릴레이션
- 4NF
- FD나 MVD가 존재하지 않음
- 어떤 공급자가 어떤 부붐을 어떤 프로젝트에 공급
 이 SN, CP ,PS를 다 각각의 릴레이션으로 만듬
=> 2개의 조인만으로 SCP를 재생성 ㄴㄴ == 3개를 조인해야함 == 3-way순환 제약 조건
이 SN, CP ,PS를 다 각각의 릴레이션으로 만듬
=> 2개의 조인만으로 SCP를 재생성 ㄴㄴ == 3개를 조인해야함 == 3-way순환 제약 조건
n-분해 릴레이션 (n>2)
n-way 순환 제약 조건을 만족
n개의 프로젝션만으로만 무손실 분해 가능 == n개보다 적으면 무손실 분해 불가능
조인 종속
몇 개의 부분 테이블로 분해한 후, 이 부분 테이블들을 다시 조인했을 때 원래의 테이블과 동일하게 복원
- MVD ㅣ JD(2 분해)
- SCP
반정규화
== 역정규화
- 분해된릴레이션을 역으로 통합 -> 성능향상
- 높은 정규형을 만족하는게 최적은아님
- 정합성과 무결성이 강화되지만
- SQL문 복잡, 조인연산 과다 -> 실행시간 오래걸림
- 중복하여추가
- 릴레이션의 병합
- 같은 속성을 중복추가
- 파생속성 추가